I’m a statistical ambassador – one of many at the Royal Statistical Society (I think that we are now on the third group). Occasionally we get interesting requests. This one came in relatively recently. Having more experience with the business end of things at festivals, I decided to volunteer for it.
Last year, I was part of a team that was based in Glastonbury during the festival, looking at the usage of generators on site. I have also been involved in running juggling / circus festivals for many years.
While I did also do simulation based tests – looking at how long a random walk through an area would need to be, on average, before getting within a specific distance of a friend (typically we used the limit of 2m) – given that your friends were also wandering around at random.
I looked at different size areas, including some trapezium shaped spaces (which would reflect the shape of a crowd in front of the stage). These simulations all lead to less conservative estimates than using the negative binomial distribution lead to. However, using the negative binomial distribution allows for a lot more situations to be investigated very quickly!
The negative binomial distribution is often used to model how many “successes” you observe before your “nth failure” – or vice versa (you just flip the probabilities). As the team at the BBC were only interested in the duration of time to find the first friend, this simplifies the calculation somewhat. The resulting article is here.
The code / output below comes straight from the html file produced using Rmarkdown. Using Rmarkdown generated html files was a very easy way of sending the code and results back and forward, where people could access the results on pretty much any device!
I used cumulative sums as the negative binomial looks at the probability of finding your friend after seeing exactly that many people, rather than at less than or equal to that many people. The code below is also designed for situations with relatively dense, large crowds, where a person will only know a very small percentage of the total crowd; it is thus not suitable for modelling how long it would take me to find someone I know at a juggling convention, where the crowds are smaller, I know a large percentage of the overall crowd, and the total crowd is much smaller than at music festivals.
In saying that, it didn’t take me long to find people I knew at Glastonbury once I wandered towards the Theatre and Circus Field!
NegBinomialSearch1<-function(p,maxsteps=40000,maxdist=maxsteps/3,crowddensity=2){
MaxFaces<-maxdist*4*(crowddensity/2)
Nstrangers<-1:MaxFaces
ret<-cumsum(p*((1-p)^Nstrangers))
return(ret)
}Initial parameters:
crowd.density<-2
MaxCrowd<-200000
p1<-(1:500)/MaxCrowd # know between 1 and 500 people, out of the total crowd
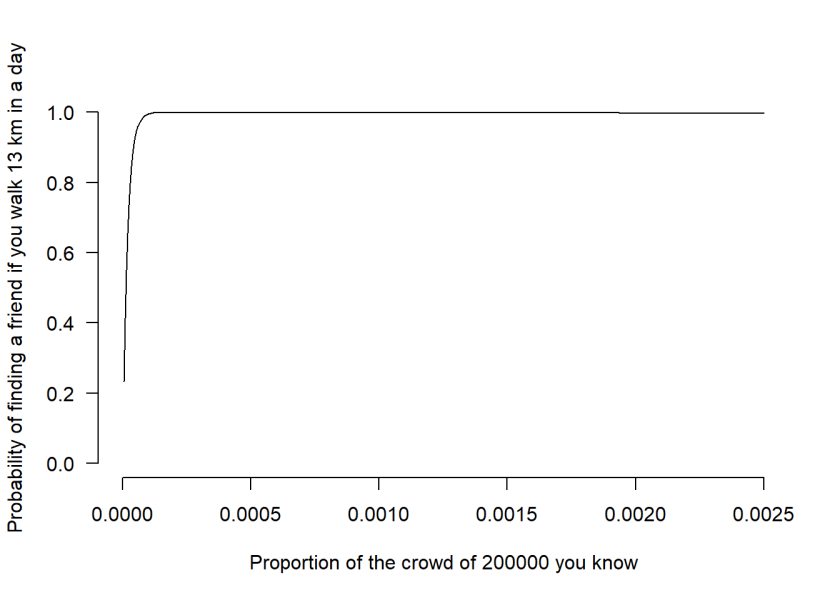
max.steps<-40000Using a crowd density of 2 per m2, and a crowd size of 200000. Using integer numbers of friends from 1 to 500, this gives a minimum probability of 0.000005 and a maximum probability of 0.0025 of a particular person being a friend.
We have also set 40000 steps as being the maximum number of steps in a given day; which is then used in the function to calculate the expected number of faces that you may encounter (so the maximum number of “attempts”). Each day starts afresh, so is treated seperately – although, in practice, these would not be fully independent, as if you would be starting from similar points each day if camping!
MF<-floor(max.steps*4*(crowd.density/6)) # how many columns needed in the matrix
PfindingFriend<-matrix(NA,length(p1),MF)
for(i in seq_along(p1)){
PfindingFriend[i,]<-NegBinomialSearch1(p1[i],maxsteps=max.steps,crowddensity=crowd.density)
}Examination of the low probabilities – when you know up to 25 people in the crowd:
Suppose:

What percentage of the crowd do you need to know to have a 99% chance of spotting someone you know?
# P(finding a friend|know x% of population) = .99, what is minimum x
min(p1[apply(PfindingFriend,1,max)>.99])## [1] 0.00009# P(finding a friend|know x% of population) = .99, what is minimum z=x*200000
min(p1[apply(PfindingFriend,1,max)>.99])*MaxCrowd## [1] 18What percentage of the crowd do you need to know to have a 99.9% chance of spotting someone you know?
# P(finding a friend|know x% of population) = .999, what is minimum x
min(p1[apply(PfindingFriend,1,max)>.999])## [1] 0.000135# P(finding a friend|know x% of population) = .999, what is minimum z=x*MaxCrowd
min(p1[apply(PfindingFriend,1,max)>.999])*MaxCrowd## [1] 27What percentage of the crowd do you need to know to have a 80% chance of spotting someone you know?
# P(finding a friend|know x% of population) = .8, what is minimum x
min(p1[apply(PfindingFriend,1,max)>.8]) # expect to spot a friend 4 out of 5 days!## [1] 0.000035# P(finding a friend|know x% of population) = .8, what is minimum z=x*MaxCrowd
min(p1[apply(PfindingFriend,1,max)>.8])*MaxCrowd # expecting to spot a friend 4 out of 5 days!## [1] 7What percentage of the crowd do you need to know to have a 50% chance of spotting someone you know?
# P(finding a friend|know x% of population) = .5, what is minimum x
min(p1[apply(PfindingFriend,1,max)>.5]) # expect to spot a friend 1 out of 2 days!## [1] 0.000015# P(finding a friend|know x% of population) = .5, what is minimum z=x*MaxCrowd
min(p1[apply(PfindingFriend,1,max)>.5])*MaxCrowd # expecting to spot a friend 1 out of 2 days!## [1] 3What percentage of the crowd do you need to know to have a 25% chance of spotting someone you know?
# P(finding a friend|know x% of population) = .25, what is minimum x
min(p1[apply(PfindingFriend,1,max)>.25]) # expect to spot a friend 1 out of 4 days!## [1] 0.00001# P(finding a friend|know x% of population) = .5, what is minimum z=x*MaxCrowd
min(p1[apply(PfindingFriend,1,max)>.25])*MaxCrowd # expecting to spot a friend 1 out of 4 days!## [1] 2Now what happens if you don’t cover the same proportion of the crowd?
If you only cover half the distance, how does that affect the minimum number of people you need to know?
ceiling(MF/2) # distance travelled## [1] 26667min(p1[apply(PfindingFriend[,1:ceiling(MF/2)],1,max)>.99])## [1] 0.000175min(p1[apply(PfindingFriend[,1:ceiling(MF/2)],1,max)>.99])*MaxCrowd## [1] 35min(p1[apply(PfindingFriend[,1:ceiling(MF/2)],1,max)>.999])## [1] 0.000275min(p1[apply(PfindingFriend[,1:ceiling(MF/2)],1,max)>.999])*MaxCrowd## [1] 55If you only cover a quarter of the distance how does that affect the minimum number of people you need to know?
ceiling(MF/4) # distance travelled## [1] 13334min(p1[apply(PfindingFriend[,1:ceiling(MF/4)],1,max)>.99])## [1] 0.00035min(p1[apply(PfindingFriend[,1:ceiling(MF/4)],1,max)>.99])*MaxCrowd## [1] 70min(p1[apply(PfindingFriend[,1:ceiling(MF/4)],1,max)>.999])## [1] 0.000585min(p1[apply(PfindingFriend[,1:ceiling(MF/4)],1,max)>.999])*MaxCrowd## [1] 117If you only cover a fifth of the distance how does that affect the minimum number of people you need to know?
ceiling(MF/5) # distance travelled## [1] 10667min(p1[apply(PfindingFriend[,1:ceiling(MF/5)],1,max)>.99])## [1] 0.00044min(p1[apply(PfindingFriend[,1:ceiling(MF/5)],1,max)>.99])*MaxCrowd## [1] 88min(p1[apply(PfindingFriend[,1:ceiling(MF/5)],1,max)>.999])## [1] 0.0008min(p1[apply(PfindingFriend[,1:ceiling(MF/5)],1,max)>.999])*MaxCrowd## [1] 160If you only cover an eight of the distance, how does that affect the minimum number of people you need to know?
ceiling(MF/8) # distance covered## [1] 6667min(p1[apply(PfindingFriend[,1:ceiling(MF/8)],1,max)>.99])## [1] 0.000705min(p1[apply(PfindingFriend[,1:ceiling(MF/8)],1,max)>.99])*MaxCrowd## [1] 141min(p1[apply(PfindingFriend[,1:ceiling(MF/8)],1,max)>.999])## Warning in min(p1[apply(PfindingFriend[, 1:ceiling(MF/8)], 1, max) >
## 0.999]): no non-missing arguments to min; returning Inf## [1] Infmin(p1[apply(PfindingFriend[,1:ceiling(MF/8)],1,max)>.999])*MaxCrowd## Warning in min(p1[apply(PfindingFriend[, 1:ceiling(MF/8)], 1, max) >
## 0.999]): no non-missing arguments to min; returning Inf## [1] Inf# don't reach the point at which we find a friend 99.9% of the time at this distance!